
 江苏省苏州中学2024-2025学年度第二学期质量评估
江苏省苏州中学2024-2025学年度第二学期质量评估
高一物理
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间75分钟。所有答案均写在答题纸上。
第Ⅰ卷(选择题,共44分)
一、单项选择题:共11题,每题4分,共计44分,每题只有一个选项最符合题意。
1. 卡文迪什巧妙地利用扭秤装置,第一次在实验室里比较准确地测出了引力常量G作为国际单位制的基本单位表示引力常量G的单位是( )
A. 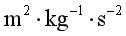 B.
B. 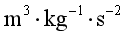
C. ![]() D.
D. ![]()
【答案】B
【解析】
【详解】根据万有引力定律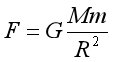
可得![]()
所以G的单位为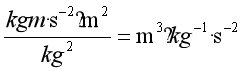
故选B。
2. 惯性系A和惯性系B相向而行,以下说法正确的是( )
A. 惯性系A中的人看惯性系B中的物理过程变快,惯性系B中的人看惯性系A中的物理过程变快
B. 惯性系A中的人看惯性系B中的物理过程变慢,惯性系B中的人看惯性系A中的物理过程变慢
C. 惯性系A中的人看惯性系B中的物理过程变快,惯性系B中的人看惯性系A中的物理过程变慢
D. 惯性系A中 人看惯性系B中的物理过程变慢,惯性系B中的人看惯性系A中的物理过程变快
人看惯性系B中的物理过程变慢,惯性系B中的人看惯性系A中的物理过程变快
【答案】B
【解析】
【详解】时间延缓效应与相对运动的方向无关,静止参考系的时间是固有时间。惯性系A与惯性系B中的人都感觉自己的参考系是静止的,在相对某参考系运动的参考系来看,原参考系中的时间就变长了,运动就变慢了。
故选B。
3. 如图所示,带有一白点的黑色圆盘,绕过其中心且垂直于盘面的轴沿顺时针方向匀速转动,转速n=10r/s。在暗室中用每秒闪光8次的频闪光源照射圆盘,则观察到白点转动的方向和转动的周期分别为( )
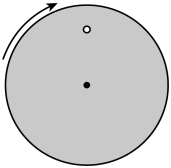
A. 顺时针转动,周期为0.2s B. 顺时针转动,周期为0.5s
C. 逆时针转动,周期为1.0s D. 逆时针转动,周期为2.0s
【答案】B
【解析】
【详解】带有一白点的黑色圆盘,绕过其中心且垂直于盘面的轴沿顺时针方向匀速转动,转速为10r/s,即f0=10Hz
在暗室中用每秒闪光8次的频闪光源照射圆盘,即f′=8Hz
由于0<f′<f0,所以观察到白点顺时针旋转,顺时针转动的频率:f=f0-f′=2Hz
所以观察到白点每秒顺时针旋转2圈,即转动周期为T=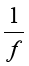 =0.5s
=0.5s
故选B。
4. 当自行车在水平路面上正常匀速前进时,轮胎边缘气门嘴的运动,可以等效成一个沿前进方向匀速直线运动和一个匀速圆周运动的合运动。关于气门嘴,下列说法正确的是( )

A. 相对于轮轴的线速度和沿前进方向匀速直线运动的速度一定相同
B. 运动到车轮轮轴前方同一水平位置时的速度方向竖直向下
C. 所受合力大小不变,方向始终指向车轮轮轴方向
D. 运动到最低点时所受合力为零
【答案】C
【解析】
【详解】A.根据
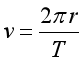
可知,相对于轮轴的线速度和沿前进方向匀速直线运动的速度大小相等,方向不同,故A错误;
B.运动到车轮轮轴前方同一水平位置时的速度方向是竖直向下和水平方向的合速度方向,不是竖直向下,故B错误;
CD.气门嘴参与匀速直线运动和匀速圆周运动两个分运动,则所受合力提供向心力,大小不变,方向始终指向车轮轮轴方向,故C正确,D错误。
故选C。
5. 如图所示,长度不同的两根轻绳L1与L2,一端分别连接质量为m1和m2的两个小球,另一端悬于天花板上的同一点O,两小球质量之比m1∶m2=1∶2,两小球在同一水平面内做匀速圆周运动,绳L1、L2与竖直方向的夹角分别为30°与60°,下列说法中正确的是( )
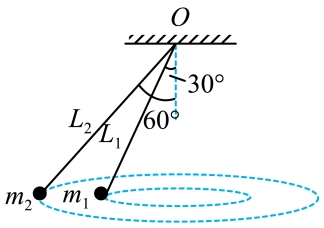
A. 绳L1、L2的拉力大小之比为1∶3
B. 小球m1、m2运动的向心力大小之比为1∶6
C. 小球 m1、m2运动的周期之比为2∶1
D. 小球 m1、m2运动的线速度大小之比为1∶2
【答案】B
【解析】
【详解】A.小球在水平面内做匀速圆周运动,设绳L1、L2的拉力大小分别为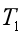 、
、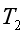 ,在竖直方向根据平衡条件可得拉力大小
,在竖直方向根据平衡条件可得拉力大小
![]()
![]()
可得绳L1、L2的拉力大小之比为
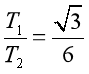
故A错误;
B.小球在水平面内做匀速圆周运动,小球m1运动的向心力大小
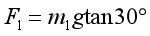
小球m2运动的向心力大小
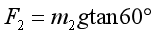
则有
![]()
故B正确;
C.小球在水平面内做匀速圆周运动,则有
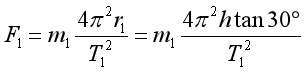
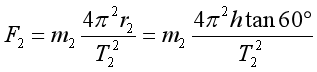
则有
![]()
故C错误;
D.小球在水平面内做匀速圆周运动,则有
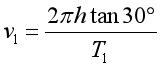
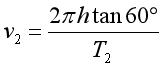
则小球 m1、m2运动的线速度大小之比为
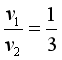
故D错误;
故选B。
6. 如图,一长l=0.5m的轻杆,一端固定在水平转轴上,另一端固定一质量m=0.5kg的小球,轻杆随转轴在竖直平面内做角速度ω=4rad/s的匀速圆周运动,其中A为最高点,C为最低点,B、D两点和圆心O在同一水平线上,重力加速度g=10m/s2,则( )
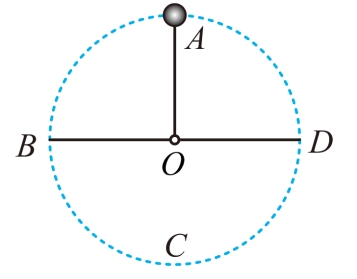
A. 小球在A点时,杆对小球的作用力方向竖直向下
B. 小球在B点时,杆对小球的作用力方向指向圆心
C. 小球在C点时,杆对小球的作用力大小为4N
D. 小球在D点时,杆对小球的作用力大小为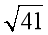 N
N
【答案】D
【解析】
【详解】小球做匀速圆周运动,合力提供向心力。
A.小球在A点时,
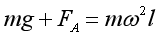
解得:
![]()
故杆对小球的作用力方向竖直向上,故A错误;
B.小球在B点时,合力提供向心力,则杆对小球的作用力方向斜向右上方,故B错误;
C.小球在C点时
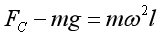
解得:
![]()
故C错误;
D.小球在D点时,杆对小球的作用力方向斜向做上方
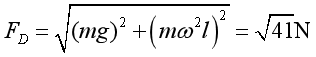
故D正确;
故选D。
7. 下列关于地球同步卫星的说法中正确的是( )
A. 仅需三颗同步卫星就可覆盖地球表面的全部区域
B. 所有同步卫星的速度都相同
C. 同步卫星距地表面的距离大约为地球半径的6.6倍
D. 同步卫星的角速度大小约为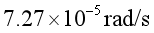
【答案】D
【解析】
【详解】A.仅需三颗同步卫星就可覆盖地球赤道的全部区域,但不能覆盖地球表面的全部区域,故A错误;
B.所有同步卫星的速度大小相等,但方向不同,故B错误;
C.同步卫星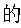 轨道半径大约为地球半径的6.6倍,则同步卫星距地表面的距离大约为地球半径的5.6倍,故C错误;
轨道半径大约为地球半径的6.6倍,则同步卫星距地表面的距离大约为地球半径的5.6倍,故C错误;
D.地球自转的角速度为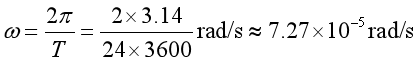
同步卫星的角速度等于地球自转的角速度,所以同步卫星的角速度大小约为![]() ,故D正确。
,故D正确。
故选D。
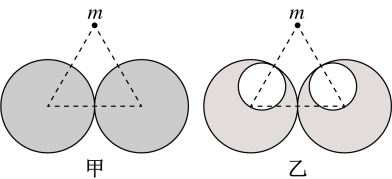
8. 如图甲所示,两个半径均为R、质量均为M的均匀球体靠在一起,与两球心相距均为2R的质点m受到两球对它的万有引力的合力F1。现紧贴球的边缘各挖去一个半径为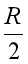 的球形空穴,如图乙所示,挖去后,质点m受到的合引力为F2,则( )
的球形空穴,如图乙所示,挖去后,质点m受到的合引力为F2,则( )
A. F2=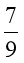 F1 B. F2=
F1 B. F2=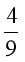 F1
F1
C. F2=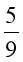 F1 D. F2=
F1 D. F2=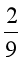 F1
F1
【答案】A
【解析】
【详解】把整个球体对质点的引力看成是挖去的小球体和剩余部分对质点的引力之和。两个完整的均质球体对球外质点m的引力这个引力为
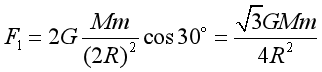
此力可以看成是挖去球穴后的剩余部分对质点的引力![]() 与两个半径为
与两个半径为![]() 的小球对m质点的引力
的小球对m质点的引力![]() 之和,即
之和,即
![]()
根据
![]()
半径为![]()
![]() 小球质量为
小球质量为
![]()
两个半径为![]() 的小球对m质点的引力为
的小球对m质点的引力为
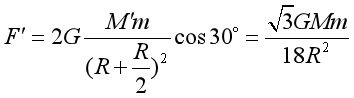
挖去球穴后的剩余部分对球外质点m的引力为
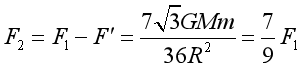
故选A。
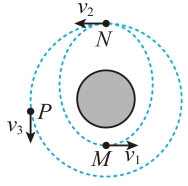
9. 在发射卫星时,往往先将卫星发送到一个椭圆轨道上,再变轨到圆轨道。已知某卫星运行的椭圆轨道的近地点M距地面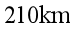 ,远地点N距地面
,远地点N距地面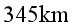 ,卫星进入该轨道正常运行时,通过M点和N点时的速率分别为
,卫星进入该轨道正常运行时,通过M点和N点时的速率分别为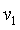 和
和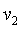 ,当某次卫星通过N点时,启动卫星上的发动机,使卫星在短时间内加速后进入离地面
,当某次卫星通过N点时,启动卫星上的发动机,使卫星在短时间内加速后进入离地面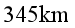 的圆形轨道,开始绕地球做匀速圆周运动,这时卫星的速率为
的圆形轨道,开始绕地球做匀速圆周运动,这时卫星的速率为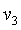 。比较卫星在M、N、P三点正常运行时(不包括启动发动机加速阶段)的速率
。比较卫星在M、N、P三点正常运行时(不包括启动发动机加速阶段)的速率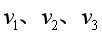 和加速度大小
和加速度大小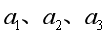 ,下列结论正确的是( )
,下列结论正确的是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
【答案】D
【解析】
【详解】根据万有引力提供向心力
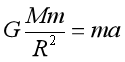
得
![]()
由题可知![]() ,所以
,所以![]() ,当某次飞船通过N点,地面指挥部发出指令,点燃飞船上的发动机,使飞船在短时间内加速后进入离地面340 km的圆形轨道绕地球做匀速圆周运动,所以
,当某次飞船通过N点,地面指挥部发出指令,点燃飞船上的发动机,使飞船在短时间内加速后进入离地面340 km的圆形轨道绕地球做匀速圆周运动,所以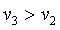 ;假设飞船在半径为
;假设飞船在半径为![]() 的圆轨道上做匀速圆周运动,经过M点时的速率为
的圆轨道上做匀速圆周运动,经过M点时的速率为![]() ,根据
,根据
![]()
得
![]()
又因为![]() ,所以
,所以![]() ,飞船在圆轨道M点时需加速才能进入椭圆轨道,则
,飞船在圆轨道M点时需加速才能进入椭圆轨道,则![]() ,故
,故![]() 。
。
故选D。
10. 20世纪人类最伟大的创举之一是开拓了太空的全新领域.现有一艘远离星球在太空中直线飞行的宇宙飞船,为了测量自身质量,启动推进器,测出飞船在短时间Δt内速度的改变为Δv,和飞船受到的推力F(其它星球对它的引力可忽略).飞船在某次航行中,当它飞近一个孤立的星球时,飞船能以速度v,在离星球的较高轨道上绕星球做周期为T的匀速圆周运动.已知星球的半径为R,引力常量用G表示.则宇宙飞船和星球的质量分别是( )
A. ![]() ,
,![]() B.
B. ![]() ,
,![]()
C. ![]() ,
,![]() D.
D. ![]() ,
,![]()
【答案】D
【解析】
 分析】根据动量定理求解飞船质量;根据牛顿第二定律与万有引力定律求解星球质量;
分析】根据动量定理求解飞船质量;根据牛顿第二定律与万有引力定律求解星球质量;
【详解】直线推进时,根据动量定理可得
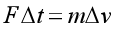
解得飞船的质量为
![]()
绕孤立星球运动时,根据公式
![]() ,
,![]()
解得
![]()
故选D。
【点睛】本题需要注意的是飞船在绕孤立星球运动时,轨道不是星球的半径,切记切记。
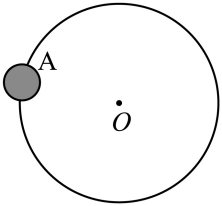
11. 经长期观测发现,A行星运行的轨道半径为R0,周期为T0,但其实际运行的轨道与圆轨道总存在一些偏离,且周期性地每隔t0时间发生一次最大的偏离.如图所示,天文学家认为形成这种现象的原因可能是A行星外侧还存在着一颗未知行星B,则行星B的运行轨道半径为( )
A. R=R0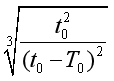 B. R=R0
B. R=R0![]()
C. R=R0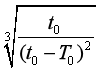 D. R=R0
D. R=R0![]()
【答案】A
【解析】
【详解】A行星运行的轨道发生最大偏离,必是B对A的引力引起的,B行星在此时刻对A有最大的力,故A、B行星与恒星在同一直线上且位于恒星同一侧.设行星B的运行周期为T,半径为R,则有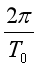 t0-
t0-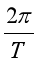 t0=2π,所以T=
t0=2π,所以T=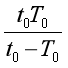 ,由开普勒第三定律得
,由开普勒第三定律得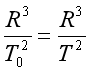 ,得R=R0
,得R=R0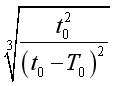 ,所以A正确.
,所以A正确.
第Ⅱ卷(非选择题,共56分)
二、非选择题:共5题,共56分。其中第13~16题解答时请写出必要的文字说明、方程式和重要的演算步骤,只写出最后答案的不能得分;有数值计算时,答案中必须明确写出数值和单位。
12. 如图所示,在验证向心力公式的实验中,质量相同的钢球①放在A盘的边缘,钢球②放在A盘边缘某点与盘中心连线的中点上,钢球③放在B盘的边缘,A、B两盘的半径之比为2:1,a、b分别是与A盘、B盘同轴的轮。a、b的轮半径之比为1:2,用皮带连接a、b两轮稳定皮带转动时,
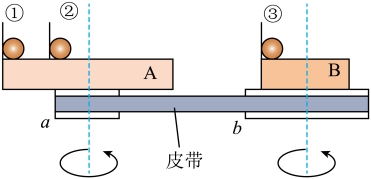
(1)钢球①、②、③的速度大小之比为___________;
(2)钢球①、②、③受到的向心力之比为___________。
某同学用如图所示的实验装置来验证向心力公式。均质小球由轻绳a和b分别系于一轻质木架上的A点和C点。当木架绕轴BC匀速转动时,小球在 ①水平面内做匀速圆周运动,绳a在竖直方向、绳b在水平方向。两绳的A、C端分别安装有拉力传感器1、2,重力加速度为g,忽略空气的阻力,实验步骤如下:

A.实验之前,用游标卡尺测得小球的直径为d,用刻度尺测得a绳的长度为la,b绳的长度为lb;
B.使木架绕BC轴匀速转动,并带动小球在水平面内做匀速圆周运动,记录转n圈对应的时间t;
C.读出拉力传感器1、2的示数分别为Fa、Fb:
D.当小球运动到图示位置时,绳b被突然烧断,同时木架也立即停止转动,读出拉力传感器1在此瞬间的示数为F0.
(3)小球的质量m=___________;
(4)绳b被烧断之前小球做匀速圆周运动,若Fb=___________,则向心力公式得到验证;(用Fa、n、t、g、lb和d等表示)
(5)绳b被烧断之后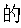 瞬间,若F0=___________,则向心力公式得到验证。(用Fa、n、t、g、la、lb和d等表示)
瞬间,若F0=___________,则向心力公式得到验证。(用Fa、n、t、g、la、lb和d等表示)
【答案】 ①. 4:2:1 ②. 8:4:1 ③. 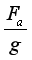 ④.
④. 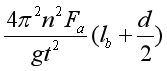 ⑤.
⑤. 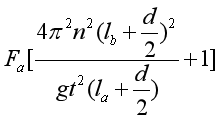
【解析】
【详解】(1)[1]设a轮转动的角速度为2ω,因ab同缘转动,则b轮转动的角速度为ω,钢球①、②、③的速度分别为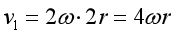 ,
,![]() ,
,![]()
即三球线速度之比为4:2:1;
(2)[2]根据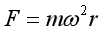 可得钢球①、②、③受到的向心力之比为
可得钢球①、②、③受到的向心力之比为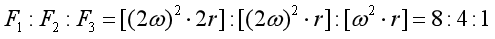
(3)[3]小球做圆周运动时,竖直方向 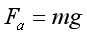
解得小球质量![]()
(4)[4] 小球做匀速圆周运动的角速度 ,绳b被烧断之前小球做匀速圆周运动,则
,绳b被烧断之前小球做匀速圆周运动,则![]() ,
,![]()
解得![]()
(5)[5]小球做匀速圆周运动的角速度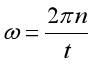
线速度:![]()
绳b被烧断之后的瞬间,小球的速度来不及突变,即将在竖直面内做变速圆周运动,半径为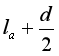 ,绳a的拉力突变为F0,向心力突变为:F0-mg,若:
,绳a的拉力突变为F0,向心力突变为:F0-mg,若: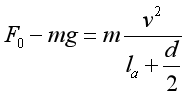 ,
,![]()
可解得
则向心力公式得到验证。
13. 某个走时准确的时钟,分针与时针由转动轴到针尖的长度之比是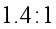 。
。
(1)分针针尖与时针针尖的线速度之比是多少?
(2)分针针尖与时针针尖的向心加速度之比是多少?
【答案】(1)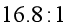
(2)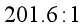
【解析】
【小问1详解】
分针的周期为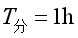 ,时针的周期为
,时针的周期为 ,根据
,根据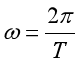
可得分针与时针的角速度之比为![]()
根据![]() ,可得分针针尖与时针针尖的线速度之比为
,可得分针针尖与时针针尖的线速度之比为![]()
【小问2详解】
根据 ,可得分针针尖与时针针尖的向心加速度之比为
,可得分针针尖与时针针尖的向心加速度之比为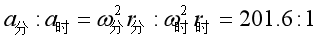
14. 如图所示,某一圆弧路段的半径为R,路面与水平面间的夹角为θ,自行车与骑手总质量为m,在该路段以某一速度做匀速圆周运动。已知路面与自行车轮之间的摩擦因数为μ,重力加速度为g,不考虑空气阻力,自行车与路面之间没有相对滑动。
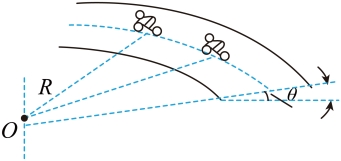
(1)若要使自行车转弯不受摩擦力作用,其速度v0大小是多少?
(2)自行车在该路面上转弯的最大速率vmax与最小速率vmin之比是多少(用μ、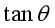 表示)?
表示)?
【答案】(1)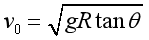
(2)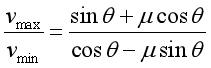
【解析】
【小问1详解】
若要使自行车转弯不受摩擦力作用,则满足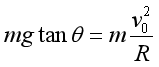
解得![]()
【小问2详解】
系统即将向外滑动时,速度最大,设最大静摩擦力为f,则有Ncosθ=fsinθ+mg,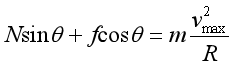
其中f=μN
解得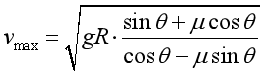
系统即将向内滑动时,速度最小,则Ncosθ+fsinθ=mg,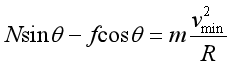
其中f=μN
解得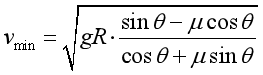
可得![]()
15. 已知某星球的半径为![]() ,自转周期为
,自转周期为![]() ,它的静止卫星到星球表面的高度为
,它的静止卫星到星球表面的高度为![]() 。已知万有引力常量为
。已知万有引力常量为![]() 。
。
(1)求该星球的密度。
(2)求该星球的第一宇宙速度。
(3)求该星球北极重力加速度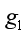 与赤道重力加速
与赤道重力加速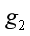 的差值。
的差值。
【答案】(1)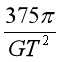 ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
【分析】
【详解】(1)由星球对静止卫星的万有引力提供其做圆周运动的向心力,设星球质量M
卫星质量m,则
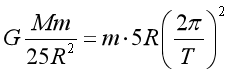
解得
![]()
由
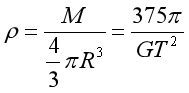
(2)由
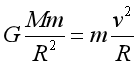
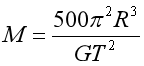
得
![]()
(3)该星球北极重力加速度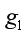 为
为
![]()
![]()
赤道重力加速![]() ,由质量为m0的物体在赤道上
,由质量为m0的物体在赤道上
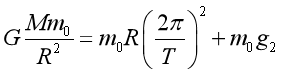
故
![]()
该星球北极重力加速度![]() 与赤道重力加速
与赤道重力加速![]() 的差值为
的差值为
![]()
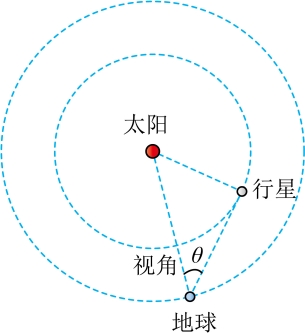
16. 如图所示,地球和某行星在同一轨道平面内同向绕太阳做匀速圆周运动。地球的运转周期为T。地球和太阳的连线与地球和行星的连线所夹的角叫地球对该行星的观察视角(简称视角)。已知该行星的最大视角为θ,当行星处于最大视角处时,是地球上天文爱好者观察该行星的最佳时期。试求:
(1)该行星绕太阳转动的周期。
(2)行星绕太阳转动的向心加速度与地球绕太阳转动的向心加速度之比。
(3)若某时刻该行星正处于最佳观察期,则该行星下一次处于最佳观察期至少需经历多长时间?
【答案】(1)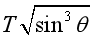
(2)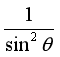
(3)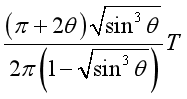 或者
或者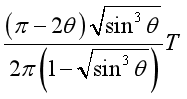
【解析】
【小问1详解】
当有最大视角时,太阳和行星的连线与地球与行星的连线垂直,设地球的轨道半径为R,则可知行星的轨道半径r为:r=Rsinθ
设行星绕太阳的运转周期为T′,由开普勒第三定律有: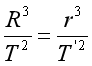
解得:![]()
【小问2详解】
根据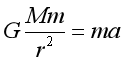
可得![]()
可得![]()
【小问3详解】
假设行星和地球绕太阳做逆时针转动,设行星最初处于最佳观察期时,其位置超前于地球,设经时间t地球转过α角,行星再次处于最佳观察期,则行星转过的角度β为:β=π+α+2θ
那么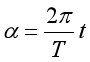 ,
,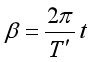
可得: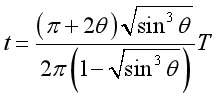
若行星最初处于最佳观察期时,行星和地球绕太阳做顺时针转动,其位置滞后于地球,同理可得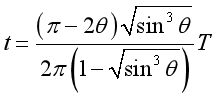
附件 (2个)
1、本网站所提供的信息,只供教育教学参考之用。
2、本网站及其会员一概毋须以任何方式就任何信息传递或传送的失误、不准确或错误对用户或任何其他人士负任何直接或间接的责任。
3、在法律允许的范围内,本网站在此声明,不承担用户或任何人士就使用或未能使用本网站所提供的信息或任何链接或项目所引致的任何直接、间接、附带、从属、特殊、惩罚性或惩戒性的损害赔偿。
4、访问者在从事与本网站相关的所有行为(包括但不限于访问浏览、利用、转载、宣传介绍)时,必须以善意且谨慎的态度行事;访问者不得故意或者过失的损害本网站的各类合法权益,不得利用本网站以任何方式直接或者间接的从事违反中华人民共和国法律、国际公约以及社会公德的行为。对于访问者利用本网站提供的信息而作出的任何决策、决定以及其后果,本网站不承担任何责任
5、本网站图片,文字之类版权,本网站无法鉴别所上传图片或文字的知识版权,如果侵犯,请及时通知我们,本网站将在第一时间及时删除。
6、凡以任何方式登录本网站或直接、间接使用本网站资料者,视为自愿接受本网站声明的约束。
GYEDU
