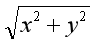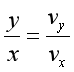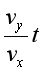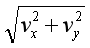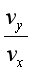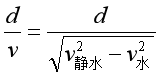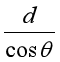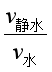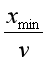GY - GYEDU

课题

5.2运动的合成与分解

教学内容分析

本节对学生的能力要求较高，着重要解决的问题是让学生建立起运动的合成与分解的思想，并用来处理简单的平面运动，为平抛与斜抛运动的研究打好基础。本节内容是学生在学习较简单的直线运动后，从定量研究直线运动规律进入定量研究曲线运动规律的转折点。虽然学生已经知道曲线运动的运动特征和受力特征，但他们不知道如何去描述曲线运动的位移、速度、加速度等运动参量。在此之前，学生已经有合力与分力的概念，力的合成与分解的知识与思想，这些对运动的合成与分解有一定的启发作用。通过本节的学习研究，学生将学会用平面坐标系描述曲线运动，并过运动的合成与分解，把复杂运动分解成几个简单的分运动，再通过研究分运动的性质来确定物体实际运动的性质和轨迹，进一步研究复杂的曲线运动。

学情分析

学生经历必修一直线运动的学习，会用直线运动规律(x-t图像与表达式)解决一些匀速直线运动与匀变速直线运动问题;通过相互作用力的学习，能进行简单的受力分析并应用平行四边形定则进行力的运算。学生具有一些生活中曲线运动的初步概念，但高一学生缺乏建模能力、分析推理归纳能力、抽象思维能力，也缺乏迁移能力，不能很好的调用已经学过的知识方法处理新问题、复杂问题。

教学目标

1.知道什么是合运动，什么是分运动。

2.理解运动的合成与分解。

3.会利用平行四边形定则计算分速度、合速度及分位移、合位移。

4.能够运用合成与分解思想分析一些实际问题。

教学

重难点

1．运动的合成与分解的法则。（重点）

2．小船过河问题。（重点难点）

3．关联速度问题。（重点难点）

教学过程

教学环节

教师活动

学生活动

设计意图

导入新课

观看视频，思考与讨论如下问题：

(1)若人在河中始终保持头朝正前方游向对岸，你认为他会在对岸的正前方到达，还是会偏向上游或下游？为什么？

(2)人在河中的运动是直线还是曲线？位移怎么变化？速度又是怎么变化呢？对类似上述的运动应该怎样分析呢？

复习与回顾：

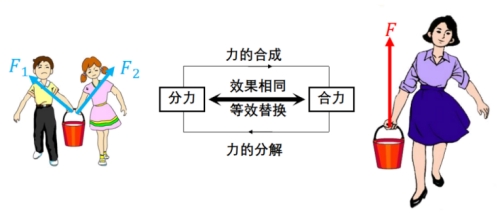
思考与讨论：

一个物体往往会受到多个力的作用，在处理物体受到多个力作用的问题时，我们需要采用力的合成或力的分解的思想方法。合成与分解的思想是解决复杂力学问题的一大利器。那么对于复杂的运动问题，我们能不能采用“合成与分解”的思想来处理呢？

学生观看思考并回答

学生回顾力的合成和分解的知识

学生思考回顾并回答

引导学生思考人的游泳参与了几个方向的运动

为运动的合成分解方法做铺垫

为运动的合成分解方法做铺垫

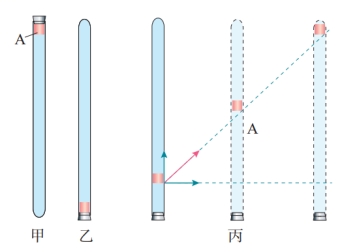
讲授新课

一、一个平面运动的实例

观看视频，思考与讨论：

(1)将放有蜡块的玻璃管倒置放在电动滑轨上，向右匀速运动，蜡块的轨迹是怎样的？如何直观的描述出蜡块每一时刻的位置和位移如何变化？

(2)将玻璃管中注满清水并倒放静置，蜡块的轨迹是怎样的？如何直观的描述出蜡块每一时刻的位置和位移如何变化？

(3)将注满水的玻璃管倒置，放置在电动滑轨上，蜡块的轨迹是怎样的？又如何直观的描述出蜡块每一时刻的位置和位移如何变化？

(4)蜡块的速度的大小、方向变化吗？如何描述？

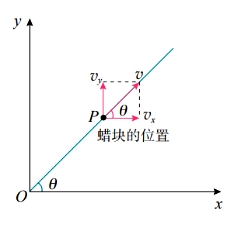
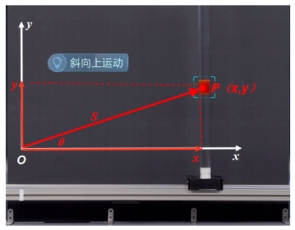
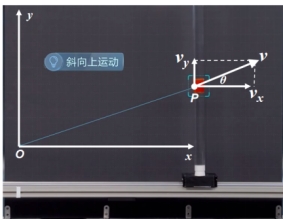
【要点总结】

1.建立坐标系

研究物体的运动时，坐标系的选取很重要。研究物体在平面内的运动时，可以选择平面直角坐标系。

在研究蜡块的运动时，我们以蜡块开始匀速运动的位置为原点O，以水平向右的方向和竖直向上的方向分别为x轴和y轴的方向，建立平面直角坐标系。

2.蜡块运动的轨迹

若以v_x表示玻璃管向右的移动速度，v_y表示蜡块沿玻璃管上升的速度，请表示蜡块在t时刻的位置及位移。

(1)x=v_xt；(2)y=v_yt；(3)s=；(4)tanθ=；(5)y=，即轨迹为直线。

3.蜡块运动的速度

(1)v=；(2)tanθ=，即速度的大小和方向保持不变，蜡块做匀速直线运动。

思考与讨论：

(1)蜡块实际的运动与水平和竖直的分运动是什么关系？

(2)蜡块A由底部运动至顶端的时间，与蜡块在竖直方向由底部运动到顶端的时间是什么关系？

(3)如果将试管以更大的速度向右运动，蜡块在竖直方向的运动情况变不变？

二、运动的合成与分解

1.合运动与分运动

    一个物体实际发生的运动产生的效果跟另外两个运动共同产生的效果相同,这一物体实际发生的运动叫做这两个运动的合运动，这两个运动叫做这以实际运动的分运动。

2.合运动与分运动的关系

(1) 等时性---合运动和分运动经历的时间相等；

(2) 独立性---各分运动独立进行，互不影响；

(3) 等效性---各分运动的规律叠加起来和合运动的规律等效。

3.运动的合成与分解

4.分解原则:一般根据运动的实际效果分解，也可以正交分解。

5.遵循规律:平行四边形法则

【例题】某商场设有步行楼梯和自动扶梯，步行楼梯每级的高度是0.15m，自动扶梯与水平面的夹角为30°，自动扶梯前进的速度是0.76m/s。有甲、乙两位顾客，分别从自动扶梯和步行楼梯的起点同时上楼，甲在自动扶梯上站立不动，乙在步行楼梯上以每秒上两个台阶的速度匀速上楼。哪位顾客先到达楼上？如果该楼层高4.56m，甲上楼用了多少时间？

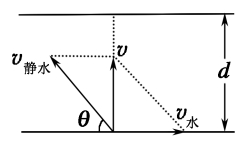
观看视频，思考与讨论：

(1)如果蜡块沿水平方向上加速运动，蜡块做什么运动？

(2)两个都是从静止开始的互成角度匀加速直线运动的合成是什么运动？

(3)两个初速度都不为零互成角度匀加速直线运动的合运动是什么运动？

三、小船过河模型

观看视频，明确两个问题：

1.小船参与的两个分运动

(1)船相对水的运动(即船在静水中的运动)，它的方向与船头的指向相同。

(2)船随水漂流的运动，它的方向与河岸平行。

2.区别三个速度：水流速度v_水、船在静水中的速度v_船、船的实际速度(即船的合速度)v_合。

思考与讨论：

(1)根据运动的合成与分解的知识，你有几种方式求小船过河的时间？用这几种方式求出的时间是否相等？

(2)你是否求出小船过河所用的最短时间呢？

3.渡河最短时间问题：

如图所示，河宽为d，v水为水流速度，v静水表示船在静水中的速度，其中v静水方向偏向上游与河岸成θ角。

思考与讨论：

(1)小船渡河时间最短时，是否小船通过的位移也是最短的？如果不是，那么在怎样的情况下小船渡河经过的位移最短呢？

(2)若v_水<v_静水时，小船渡河要位移最短，需要满足什么条件？

(3)若v_水>v_静水时，小船渡河要位移最短，需要满足什么条件？

4.渡河最小位移问题

(1)当v_水<v_静水时，

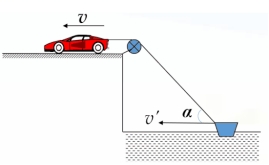
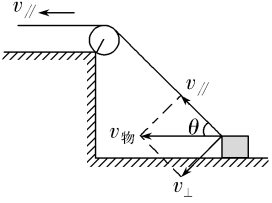
1)条件：

①船头应指向河的上游；

②v_水－v_静水cosθ＝0，即船的合速度v的方向与河岸垂直

2)最短位移：即为河的宽度d

3)渡河时间：t=

(2)当v_水>v_静水时，

1)条件：当v_静水方向与合速度v 方向垂直时，有最短渡河位移x_min 。

2)最短位移：x_min=；cosθ=

3)渡河时间：t=

四、关联速度模型

思考与讨论：

    如图所示，汽车以恒定速率v 沿水平方向通过绳子牵引小船靠岸，当绳与水面夹角为α 时，船的速度v’为多大？

【要点总结】

1.关联速度问题：一般是指物拉绳(或杆)和绳(或杆)拉物问题。高中阶段研究的绳都是不可伸长的，杆都是不可伸长且不可压缩的，即绳或杆的长度不会改变。绳、杆等连接的两个物体在运动过程中，其速度通常是不一样的，但两个物体沿绳或杆方向的速度大小相等，我们称之为关联速度。

2.解决关联速度问题的一般步骤：

第一步：先确定合运动，即物体的实际运动。

第二步：确定合运动的两个实际作用效果，一是沿绳(或杆)方向的平动效果，改变速度的大小；二是沿垂直于绳(或杆)方向的转动效果，改变速度的方向。即将实际速度正交分解为垂直于绳(或杆)和平行于绳(或杆)方向的两个分量并作出运动矢量图。

第三步：根据沿绳(或杆)方向的速度相等列方程求解。

3.常见的两种模型：

(1)绳牵联模型

①单个物体的绳子末端速度分解：如图甲所示，v_⊥一定要正交分解在垂直于绳子方向，这样v_∥的大小就是拉绳的速率，注意切勿将绳子速度分解。

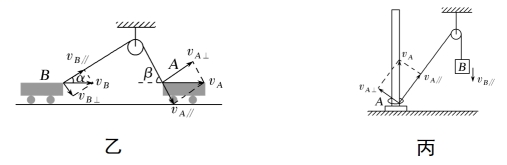
②两个物体的绳子末端速度分解：如图乙所示两个物体的速度都需要正交分解，其中两个物体的速度沿着绳子方向的分速度是相等的，即v_A∥＝v_B∥。如图丙所示，将圆环的速度分解成沿绳方向和垂直于绳方向的分速度，B的速度与A沿绳方向的分速度相等，即v_A∥＝v_B∥。

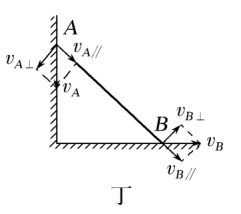
(2)杆牵联模型

    如图丁所示，将杆连接的两个物体的速度沿杆和垂直于杆的方向正交分解，则两个物体沿杆方向的分速度大小相等，即v_A∥＝v_B∥。

五、课堂练习

学生观看视频

思考蜡块位置、位移、速度的变化及描述方法

学生绘制坐标系

学生推导两个方向的位移大小和蜡块轨迹

学生推导合速度大小和方向

学生思考与讨论

学生识记记录

学生识记记录

学生识记记录

学生练习

学生观看视频思考讨论问题并回答

学生观看视频

学生记忆

学生思考讨论

学生推导

学生思考讨论并回答

学生推导

学生识记记录

学生画图验证

学生思考讨论

学生记录记忆关联速度定义

学生记录记忆关联速度求解步骤

学生记录记忆绳的关联速度分解合成方式

学生记录记忆杆的关联速度分解合成方式

学生练习

让学生直观看到蜡块的运动

让学生明确研究曲线运动的首先要建立坐标系，分方向研究

让学生定量推导位移大小、方向和轨迹

让学生定量推导速度大小和方向

为合运动和分运动定义和特点做铺垫

让学生明确定义

让学生明确两个运动的特性

让学生明确合成和分解的方法

巩固强化

为两个初速度都不为零互成角度匀加速直线运动的合运动是什么运动做铺垫

让学生直观了解小船参与的运动

为渡河最短时间推导做铺垫

明确渡河最短时间条件

为渡河最短位移做铺垫

让学生明确渡河最短位移条件

巩固强化

强化巩固

为关联速度的特点做铺垫

让学生明确关联速度定义

让学生记录明确关联速度求解步骤

学生明确绳的关联速度分解合成方式

学生明确杆的关联速度分解合成方式

巩固强化

课堂总结

板书设计

§5.2运动的合成与分解

一、一个平面运动的实例

1.建立坐标系

2.蜡块运动的轨迹：轨迹为直线

二、运动的合成与分解

1.合运动与分运动

2.合运动与分运动的关系

(1) 等时性；(2) 独立性；(3) 等效性。

3.运动的合成与分解

4.分解原则:一般根据运动的实际效果分解，也可以正交分解。

5.遵循规律:平行四边形法则

三、小船过河模型

1.小船渡河最短时间

2.渡河最小位移

四、关联速度模型

作业设计

教学反思与评价