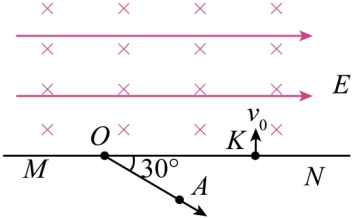
如图所示，直线MN上方各处都有水平向右的匀强电场和垂直于纸面向里的匀强磁场，匀强电场的电场强度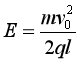
，MN下方未知的区域内存在匀强磁场，其磁感应强度大小和方向均与直线MN上方的磁场相同。放射性粒子源O沿与MN成
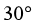斜向下的方向持续发出大量质量为m、电荷量为
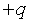的粒子，粒子沿直线运动
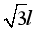的距离后从A点进入磁场（沿OA运动时，还未进入磁场），所有粒子速度大小在
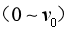范围内，经磁场偏转后所有粒子均垂直MN进入上方的区域。已知速度为
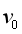的粒子离开A点后到达MN之前一直在磁场中运动，经过直线MN上的K点垂直MN进入上方区域。不计粒子的重力和粒子间的相互作用等影响，求
(1)MN下方匀强磁场的磁感应强度；
(2)速度为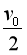
的粒子在MN下方运动的总时间；
(3)某时刻，速度分别为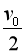
和
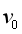的两个粒子同时通过MN进入上方区域，这两个粒子在MN上方相距的最小距离。
【答案】(1)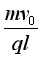
(2)
(3)
【详解】（1）作出速度为
的粒子进入MN下方磁场的运动轨迹，如图所示。
根据几何关系可得
（2分）
粒子在磁场中做匀速圆周运动，根据洛伦兹力提供向心力
（2分）
解得
（1分）
（2）速度为
的粒子在MN下方运动磁场的运动轨迹，根据
（1分）
解得
（1分）
可知该粒子在MN下方的运动分三段，即在OA段做匀速直线运动、在磁场中做匀速圆周运动，从磁场飞出后匀速直线运动从直线MN上的某点垂直MN进入上方区域，如图所示。
设OA段运动时间为
，在MN下方某区域磁场做匀速圆周运动时间为
，从磁场飞出后运动时间为
，
在OA段有
解得
（1分）
在MN下方某区域磁场做匀速度圆周，根据几何关系可知粒子偏转的圆心角为
则粒子在MN下方某区域磁场中运动的时间为
又
解得
（1分）
从磁场飞出后匀速直线运动从直线MN上的某点垂直MN进入上方区域有
解得
故速度为
的粒子在MN下方运动的总时间
（1分）
（3）方法一：设两粒子经过直线MN的点之间的距离
，根据几何关系有
两粒子在x轴方向的距离
（1分）
又 
（1分）
两粒子在y轴方向的距离
（1分）
设两粒子之间的距离为d 
解得
（1分）
两粒子间距离的最小值
（1分）
方法二：取速度为
的粒子为参考系，在此参考系下，从K点进入的粒子做线速度为
的匀速圆周运动，其位置关系如图所示。
图中P为
的粒子的位置，则两粒子之间的最小距离为圆周上点到P的最小距离
。
1、本网站所提供的信息，只供教育教学参考之用。
2、本网站及其会员一概毋须以任何方式就任何信息传递或传送的失误、不准确或错误对用户或任何其他人士负任何直接或间接的责任。
3、在法律允许的范围内，本网站在此声明,不承担用户或任何人士就使用或未能使用本网站所提供的信息或任何链接或项目所引致的任何直接、间接、附带、从属、特殊、惩罚性或惩戒性的损害赔偿。
4、访问者在从事与本网站相关的所有行为(包括但不限于访问浏览、利用、转载、宣传介绍)时，必须以善意且谨慎的态度行事；访问者不得故意或者过失的损害本网站的各类合法权益，不得利用本网站以任何方式直接或者间接的从事违反中华人民共和国法律、国际公约以及社会公德的行为。对于访问者利用本网站提供的信息而作出的任何决策、决定以及其后果，本网站不承担任何责任
5、本网站图片，文字之类版权，本网站无法鉴别所上传图片或文字的知识版权，如果侵犯，请及时通知我们，本网站将在第一时间及时删除。
6、凡以任何方式登录本网站或直接、间接使用本网站资料者，视为自愿接受本网站声明的约束。
GYEDU
