

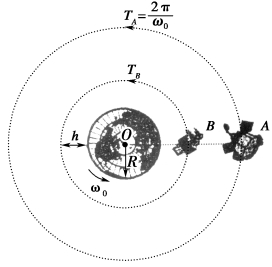
 专题06 人造卫星 双星模型
专题06 人造卫星 双星模型

考点1 卫星参数的比较
考点2 变轨问题
考点3 天体的追及相遇问题
考点4 双星模型

考点一 卫星参数的比较
人造卫星
1、地球静止轨道卫星的6个“一定”
轨道面一定 | 轨道平面与赤道平面共面 |
周期一定 | 与地球自转周期相同,即T=24 h |
角速度一定 | 与地球自转的角速度相同 |
高度一定 | 由G()R+h2=mT2(R+h)得同步卫星离地面的高度h= 4π2-R≈6R(恒量) |
速率一定 | 运行速率v=R+h |
绕行方向一定 | 与地球自转的方向一致 |
2、地球静止轨道卫星与同步卫星的关系
地球同步卫星位于地面上方,其离地面高度约为 36 000 km,周期与地球自转周期相同,但轨道平面与绕行方向可以是任意的。地球静止轨道卫星是一种特殊的同步卫星。
3、规律方法
如图所示,a为近地卫星,轨道半径为r1;b为地球同步卫星,轨道半径为r2;c为赤道上随地球自转的物体,轨道半径为r3。
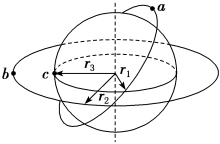
比较项目 | 近地卫星 (r1、ω1、v1、a1) | 同步卫星 (r2、ω2、v2、a2) | 赤道上随地球自转的物体 (r3、ω3、v3、a3) |
向心力 | 万有引力 | 万有引力 | 万有引力的一个分力 |
轨道半径 | r2>r1=r3 | ||
角速度 | 由Gr2=mω2r得ω=r3,故ω1>ω2 | 同步卫星的角速度与地球自转角速度相同,故ω2=ω3 | |
ω1>ω2=ω3 | |||
线速度 | 由Gr2=mr得v= r,故v1>v2 | 由v=rω得v2>v3 | |
v1>v2>v3 | |||
向心加速度 | 由Gr2=ma得a=r2,故a1>a2 | 由a=ω2r得 a2>a3 | |
1.(多选)我国发射了宇宙探测卫星“慧眼”,卫星携带了X射线调制望远镜,在离地550 km的轨道上观察遥远天体发出的X射线,为宇宙起源研究提供新的证据,则卫星的( )
A.角速度大于地球自转角速度
B.线速度小于第一宇宙速度
C.周期大于同步卫星的周期
D.向心加速度小于地面的重力加速度
答案 ABD
解析 万有引力提供向心力Gr2=mT2r
解得T=2πGM
该卫星的轨道半径小于同步卫星的轨道半径,同步卫星相对地球静止,则T<T同步=T地球,选项C错误;
根据ω=T可知ω>ω同步=ω地球,A正确;
万有引力提供向心力Gr2=mr
解得v=r
第一宇宙速度为卫星贴近地球表面运行的速度大小,该卫星的轨道半径大于地球半径,所以该卫星线速度小于第一宇宙速度,B正确;
万有引力提供加速度Gr2=ma
解得a=r2
贴近地表运行的卫星的向心加速度近似等于地表的重力加速度,该卫星的轨道半径大于地球半径,所以该卫星向心加速度小于地面的重力加速度,D正确。
2.(多选)关于环绕地球运行的卫星,下列说法正确的是( )
A.分别沿圆轨道和椭圆轨道运行的两颗卫星,可能具有相同的周期
B.沿椭圆轨道运行的一颗卫星,在轨道不同位置可能具有相同的速率
C.在赤道上空运行的两颗地球同步卫星,它们的轨道半径有可能不同
D.沿不同轨道经过北京上空的两颗卫星,它们的轨道平面一定会重合
答案AB
解析 分别沿圆轨道和椭圆轨道运行的两颗卫星,可能具有相同的周期,故A正确;沿椭圆轨道运行的一颗卫星,在轨道对称的不同位置具有相同的速率,故B正确;根据万有引力提供向心力,列出等式:G(R+h)2=m(R+h)T2,其中R为地球半径,h为同步卫星离地面的高度。由于同步卫星的周期必须与地球自转周期相同,所以T为一定值,根据上面等式得出:同步卫星离地面的高度h也为一定值,故C错误;沿不同轨道经过北京上空的两颗卫星,它们的轨道平面不一定重合,但圆心都在地心,故D错误。
3.如图所示是在同一轨道平面上的三颗不同的人造地球卫星,关于各物理量的关系,下列说法正确的是( )
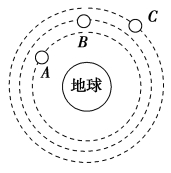
A.根据v=可知vA<vB<vC
B.根据万有引力定律可知FA>FB>FC
C.角速度ωA>ωB>ωC
D.向心加速度aA<aB<aC
答案C
解析 由题图知三颗不同的人造地球卫星的轨道半径关系为rA<rB<rC,由万有引力提供向心力得r2=mr=mrω2=ma可知v=r,所以vA>vB>vC,选项A错误;由于三颗卫星的质量关系不确定,故万有引力大小不确定,选项B错误;ω=r3,所以ωA>ωB>ωC,选项C正确;a=r2,所以aA>aB>aC,选项D错误。
4.(多选)如图所示,赤道上空的卫星A距地面高度为R,质量为m的物体B静止在地球表面的赤道上,卫星A绕行方向与地球自转方向相同。已知地球半径也为R,地球自转角速度为ω0,地球的质量为M,引力常量为G。若某时刻卫星A恰在物体B的正上方(已知地球同步卫星距地面高度比卫星A大很多),下列说法正确的是( )
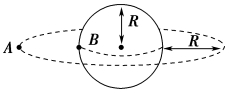
A.物体B与卫星A的向心加速度大小之比为0
B.卫星A的线速度为2ω0R
C.卫星A的角速度大于ω0
D.物体B受到地球的引力为mRω0
答案AC
解析 卫星A运动过程中,万有引力充当向心力,故有G(2R)2=maA,解得aA=4R2,物体B的向心加速度aB=ω0R,因此向心加速度之比为aA=0,A正确;绕地卫星受到的万有引力提供向心力,r2=mω2r,解得ω=r3,和同步卫星相比,卫星A的轨道半径远小于同步卫星轨道半径,故卫星A的运行角速度大于同步卫星的运行角速度,而同步卫星的运行角速度和地球自转角速度相等,所以卫星A的角速度大于ω0,C正确;卫星A的线速度v=ω·2R>ω0·2R,B错误;物体B受到万有引力分解为两部分,一部分为重力,一部分为随地球自转需要的向心力,而向心力为mω0R,所以两者不等,D错误。
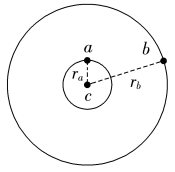
5.“太空电梯”的概念最初出现在1895年,由康斯坦丁·齐奥尔科夫斯基提出。如今,目前世界上已知的强度最高的材料——石墨烯的发现使“太空电梯”制造成为可能,人类将有望通过“太空电梯”进入太空。设想在地球赤道平面内有一垂直于地面并延伸到太空的轻质“太空电梯”,如图所示,假设某物体b乘坐太空电梯到达了图示位置并相对电梯静止,与同高度运行的卫星a、更高处同步卫星c相比较。下列说法正确的是( )

A.a与b都是高度相同的人造地球卫星
B.b的线速度小于c的线速度
C.b的线速度大于a的线速度
D.b的加速度大于a的加速度
答案B
解析 a是人造地球卫星,但b不是,故A错误;b与c的角速度相同,但b运动半径小于c运动半径,所以b的线速度小于c的线速度,故B正确;b与c的角速度相同,a的角速度大于c的角速度,故b的角速度小于a的角速度,又由于a、b做圆周运动的半径相同,故b的线速度小于a的线速度,b的加速度小于a的加速度,故C、D错误。
考点2 变轨问题
1.变轨原理及过程
(1)为了节省能量,在赤道上顺着地球自转方向发射卫星到圆轨道Ⅰ上,如图所示。
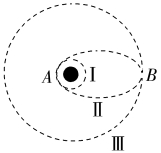
(2)在A点(近地点)点火加速,由于速度变大,万有引力不足以提供卫星在轨道Ⅰ上做圆周运动的向心力,卫星做离心运动进入椭圆轨道Ⅱ。
(3)在B点(远地点)再次点火加速进入圆形轨道Ⅲ。
2.各物理量的比较
(1)两个不同轨道的“切点”处线速度不相等。图中vⅢB>vⅡB,vⅡA>vⅠA。
(2)同一个椭圆轨道上近地点和远地点的线速度大小不相等。从远地点到近地点万有引力对卫星做正功,卫星的动能增大(引力势能减小)。图中vⅡA>vⅡB,EkⅡA>EkⅡB,EpⅡA<EpⅡB。

(3)两个不同圆轨道上线速度大小不相等。轨道半径越大,线速度越小,图中vⅠ>vⅢ。
(4)卫星在不同轨道上的机械能E不相等,“高轨高能,低轨低能”。卫星变轨过程中机械能不守恒。图中EⅠ<EⅡ<EⅢ。
(5)卫星运行的加速度与卫星和中心天体间的距离有关,与轨道形状无关,图中aⅢB=aⅡB,aⅡA=aⅠA。
6.(2024广东清远诊断)2021年1月,“天通一号”03星发射成功。发射过程简化为如图所示:火箭先把卫星送上轨道1(椭圆轨道,P、Q是远地点和近地点)后火箭脱离;卫星再变轨,到轨道2(圆轨道);卫星最后变轨到轨道3(同步圆轨道)。轨道1、2相切于P点,轨道2、3相交于M、N两点,忽略卫星质量变化,下列说法正确的是( )
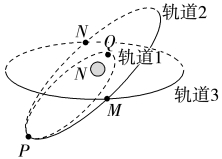
A.卫星在三个轨道上的周期T3>T2>T1
B.由轨道1变至轨道2,卫星在P点向前喷气
C.卫星在三个轨道上机械能E3=E2>E1
D.卫星在轨道1的Q点的线速度小于在轨道3的线速度
答案C
解析 根据开普勒第三定律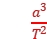 =k可知,卫星在三个轨道上的周期T3=T2>T1,故A错误;由轨道1变至轨道2做离心运动,卫星在P点向后喷气,故B错误;由轨道1变至轨道2做离心运动,卫星在P点向后喷气,机械能增大,而在轨道2、3上,高度相同,根据v=
=k可知,卫星在三个轨道上的周期T3=T2>T1,故A错误;由轨道1变至轨道2做离心运动,卫星在P点向后喷气,故B错误;由轨道1变至轨道2做离心运动,卫星在P点向后喷气,机械能增大,而在轨道2、3上,高度相同,根据v= 可知,速度大小相同,动能相同,则机械能相同,故E3=E2>E1,故C正确;卫星在轨道1的Q点的线速度大于对应圆轨道的线速度,根据v=
可知,速度大小相同,动能相同,则机械能相同,故E3=E2>E1,故C正确;卫星在轨道1的Q点的线速度大于对应圆轨道的线速度,根据v= 可知卫星在Q点对应圆轨道的线速度大于在轨道3的线速度,故卫星在轨道1的Q点的线速度大于在轨道3的线速度,故D错误。
可知卫星在Q点对应圆轨道的线速度大于在轨道3的线速度,故卫星在轨道1的Q点的线速度大于在轨道3的线速度,故D错误。
7.“神舟十一号”飞船与“天宫二号”空间实验室在太空中自动交会对接成功,是我国航天史上的一个重要里程碑。假设“天宫二号”与“神舟十一号”都围绕地球做匀速圆周运动,为了实现飞船与空间实验室的对接,下列措施可行的是( )

A.使飞船与空间实验室在同一轨道上运行,然后飞船加速追上空间实验室实现对接
B.使飞船与空间实验室在同一轨道上运行,然后空间实验室减速等待飞船实现对接
C.飞船先在比空间实验室半径小的轨道上加速,加速后飞船逐渐靠近空间实验室,两者速度接近时实现对接
D.飞船先在比空间实验室半径小的轨道上减速,减速后飞船逐渐靠近空间实验室,两者速度接近时实现对接
答案C
解析 若使飞船与空间实验室在同一轨道上运行,然后飞船加速,所需向心力变大,则飞船将脱离原轨道而进入更高的轨道,不能实现对接,A错误;若使飞船与空间实验室在同一轨道上运行,然后空间实验室减速,所需向心力变小,则空间实验室将脱离原轨道而进入更低的轨道,不能实现对接,B错误;要想实现对接,可使飞船在比空间实验室半径较小的轨道上加速,飞船将进入较高的空间实验室轨道,逐渐靠近空间实验室后,两者速度接近时实现对接,C正确;若飞船在比空间实验室半径较小的轨道上减速,则飞船将进入更低的轨道,不能实现对接,D错误。
8.我国在西昌卫星发射中心发射“中星9A”广播电视直播卫星,按预定计划,“中星9A”应该首先被送入近地点约为200公里,远地点约为3.6万公里的转移轨道Ⅱ(椭圆),然后通过远地点Q变轨,最终进入地球同步轨道Ⅲ(圆形)(如图所示)。但是由于火箭故障,卫星实际入轨后初始轨道远地点只有1.6万公里,科技人员没有放弃,通过精心操作,利用卫星自带燃料在近地点点火,尽量抬高远地点的高度,经过10次轨道调整,终于将其成功定位于预定轨道,下列说法正确的是( )
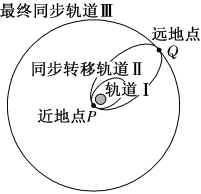
A.卫星从轨道Ⅰ的P点进入轨道Ⅱ后机械能不变
B.卫星在轨道Ⅲ经过Q点时和轨道Ⅱ经过Q点时的速度相同
C.卫星在轨道Ⅰ经过P点时和轨道Ⅱ经过P点时的加速度相同
D.“中星9A”发射失利原因可能是发射速度没有达到7.9 km/s
答案 C
解析 卫星从轨道Ⅰ变轨到轨道Ⅱ轨道半径变大,要做离心运动,卫星应从轨道Ⅰ的P点加速后才能做离心运动从而进入轨道Ⅱ,卫星加速过程机械能增加,故A错误;卫星由Ⅱ的Q点加速后才能进入Ⅲ,由此可知,卫星在轨道Ⅲ经过Q点时的速度大于轨道Ⅱ经过Q点时的速度,故B错误;根据牛顿第二定律可知,在同一个点卫星所受的万有引力相同,故卫星在不同轨道上的同一点P上的加速度相同,故C正确;卫星的最小发射速度为7.9 km/s,卫星已经发射,失利原因不可能是发射速度没有达到7.9 km/s,故D错误。
9.(多选)若“嫦娥五号”从距月面高度为100 km的环月圆形轨道Ⅰ上的P点实施变轨,进入近月点为15 km的椭圆轨道Ⅱ,由近月点Q落月,如图所示。关于“嫦娥五号”,下列说法正确的是( )
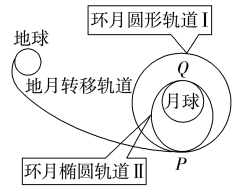
A.沿轨道Ⅰ运动至P时,需制动减速才能进入轨道Ⅱ
B.沿轨道Ⅱ运行的周期大于沿轨道Ⅰ运行的周期
C.沿轨道Ⅱ运行时,在P点的加速度大于在Q点的加速度
D.在轨道Ⅱ上由P点运行到Q点的过程中,机械能不变
答案 AD
解析 要使“嫦娥五号”从环月圆形轨道Ⅰ上的P点实施变轨进入椭圆轨道Ⅱ,需制动减速做近心运动,A正确;由开普勒第三定律知,沿轨道Ⅱ运行的周期小于沿轨道Ⅰ运行的周期,B错误;根据万有引力提供向心力可得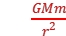 =ma,则沿轨道Ⅱ运行时,在P点的加速度小于在Q点的加速度,C错误;月球对“嫦娥五号”的万有引力指向月球,所以在轨道Ⅱ上由P点运行到Q点的过程中,万有引力对其做正功,它的动能增加,重力势能减小,机械能不变,D正确。
=ma,则沿轨道Ⅱ运行时,在P点的加速度小于在Q点的加速度,C错误;月球对“嫦娥五号”的万有引力指向月球,所以在轨道Ⅱ上由P点运行到Q点的过程中,万有引力对其做正功,它的动能增加,重力势能减小,机械能不变,D正确。
10.(2023湛江测试一)2022年11月30日,“神舟十五号”载人飞船与“天和”核心舱完成对接,航天员费俊龙、邓清明、张陆进入“天和”核心舱.对接过程的示意图如图所示,“天和”核心舱处于半径为r3的圆轨道Ⅲ;“神舟十五号”飞船处于半径为r1的圆轨道Ⅰ,运行周期为T1,通过变轨操作后,沿椭圆轨道Ⅱ运动到B处与“天和”核心舱对接,则“神舟十五号”飞船( )
A.由轨道Ⅱ进入轨道Ⅲ需在B点减速
B.沿轨道 Ⅱ 运行的周期为T2=T13
C.在轨道Ⅰ上A点的加速度大于在轨道Ⅱ上A点的加速度
D.在轨道Ⅲ上B点的线速度大于在轨道Ⅱ上B点的线速度
答案 D
解析 由低轨道进入高轨道需要点火加速,所以轨道Ⅱ进入轨道Ⅲ需在B点加速,故A错误;根据开普勒第三定律,有11=2,解得T2=T13,故B错误;由于在轨道Ⅰ、Ⅱ上A点的万有引力相同,加速度也相同,故C错误;由轨道Ⅱ进入轨道Ⅲ需在B点加速,所以在轨道Ⅲ上B点的线速度大于在轨道Ⅱ上B点的线速度,故D正确.
考点3 天体的追及相遇问题
1.相距最近
当两卫星相距最近,从运动关系上,两卫星的角度关系为(ωA-ωB)t=2πn(n=1,2,3,…)(同向)或(ωA+ωB)t=2πn(n=1,2,3,…)(反向),两卫星转过的圈数关系为 -
- =n(n=1,2,3,…)(同向)或
=n(n=1,2,3,…)(同向)或 +
+ =n(n=1,2,3,…)(反向)。
=n(n=1,2,3,…)(反向)。
2.相距最远
当两卫星位于和中心连线的半径上两侧时,两卫星相距最远,从运动关系上,两卫星运动角度关系应满足(ωA-ωB)t′=(2n-1)π(n=1,2,3,…)(同向),或(ωA+ωB)t′=(2n-1)π(n=1,2,3,…)(反向)。两卫星转过的圈数关系为 -
- =
=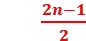 (n=1,2,3,…)(同向),或
(n=1,2,3,…)(同向),或 +
+ =
=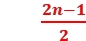 (n=1,2,3,…)(反向)。
(n=1,2,3,…)(反向)。
11.(多选)假设三颗卫星a、b、c均在赤道平面上空绕地球做匀速圆周运动,其中a、b转动方向与地球自转方向相同,c转动方向与地球自转方向相反,a、b、c三颗卫星的周期分别为Ta=6 h、Tb=24 h、Tc=12 h,某一时刻三个卫星位置如图所示.从该时刻起,下列说法中正确的是( )
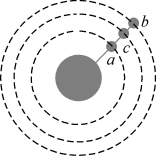
A.a、b每经过4 h相距最近一次
B.a、b经过8 h第一次相距最远
C.a、c经过2 h第一次相距最远
D.a、c经过8 h相距最近
答案CD
解析 a、b转动方向相同,在相遇一次的过程中,a比b多转一圈,设相遇一次的时间为t1,由Ta-Tb=1,解得 t1=8 h,a、b每经过8 h相距最近一次,故A、B错误;a、c转动方向相反,设经过时间t2 a、c第一次相距最远,则Ta+Tc=2,解得t2=2 h,C正确;a、c转动方向相反,在相距最近的过程中,a、c共转n圈,设相遇的时间为t2,则由Ta+Tc=n(n=1,2,3,…),当n=2,t2=8 h,故D正确.
12.(2023湖北卷)2022年12月8日,地球恰好运行到火星和太阳之间,且三者几乎排成一条直线,此现象被称为“火星冲日”.火星和地球几乎在同一平面内沿同一方向绕太阳做圆周运动,火星与地球的公转轨道半径之比约为3∶2,如图所示.根据以上信息可以得出( )
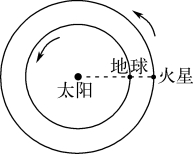
A.火星与地球绕太阳运动的周期之比约为27∶8
B.当火星与地球相距最远时,两者的相对速度最大
C.火星与地球表面的自由落体加速度大小之比约为9∶4
D.下一次“火星冲日”将出现在2023年12月8日之前
答案B
解析 火星和地球均绕太阳运动,由于火星与地球的轨道半径之比约为3∶2,根据开普勒第三定律有火地=火地,可得T地=火地=2,故A错误;火星和地球绕太阳做匀速圆周运动,速度大小均不变,当火星与地球相距最远时,由于两者的速度方向相反,故此时两者相对速度最大,故B正确;在星球表面根据万有引力等于重力有Gr2=mg,由于不知道火星和地球的质量比,故无法得出火星和地球表面的自由落体加速度关系,故C错误;火星和地球绕太阳做匀速圆周运动,有ω火=T火,ω地=T地,要发生下一次火星冲日,则有T火t=2π,解得t=T火-T地>T地,可知下一次“火星冲日”将出现在2023年12月8日之后,故D错误.
13.(2023广雅中学)如图所示,A、B为地球的两个轨道共面的人造卫星,运行方向相同,A为地球同步卫星,A、B两卫星的轨道半径的比值为k,地球自转周期为T0.某时刻A、B两卫星距离达到最近,从该时刻起到A、B间距离最远所经历的最短时间为( )
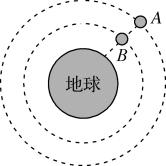
A.+1B.-1
C.-1D.+1
答案C
解析 由开普勒第三定律得AA=BB,设两卫星至少经过时间t距离最远,即B比A多转半圈,TB-TA=2,又由A是地球同步卫星知TA=T0,联立解得t=-1,故选C.
14.(多选)(2024广东汕头质检)如图所示,在万有引力作用下,a、b两卫星在同一平面内绕某一行星c沿逆时针方向做匀速圆周运动,已知轨道半径之比为ra∶rb=1∶4,则下列说法中正确的有( )
A.a、b运动的周期之比为Ta∶Tb=1∶8
B.a、b运动的周期之比为Ta∶Tb=1∶4
C.从图示位置开始,在b转动一周的过程中,a、b、c共线12次
D.从图示位置开始,在b转动一周的过程中,a、b、c共线14次
答案 AD
解析 根据开普勒第三定律,半径的三次方与周期的二次方成正比,则a、b运动的周期之比为1∶8,A正确,B错误;设图示位置ac连线与bc连线的夹角为θ< ,b转动一周(圆心角为2π)的时间为Tb,则a、b相距最远时
,b转动一周(圆心角为2π)的时间为Tb,则a、b相距最远时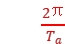 t1-
t1-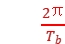 t1=(π-θ)+n·2π(n=0,1,2,…),其中t1≤Tb,可知n<6.75,n可取7个值;a、b相距最近时
t1=(π-θ)+n·2π(n=0,1,2,…),其中t1≤Tb,可知n<6.75,n可取7个值;a、b相距最近时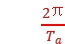 t2-
t2-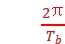 t2=(2π-θ)+m·2π(m=0,1,2,…),其中t2≤Tb,可知m<6.25,m可取7个值,故在b转动一周的过程中,a、b、c共线14次,C错误,D正确。
t2=(2π-θ)+m·2π(m=0,1,2,…),其中t2≤Tb,可知m<6.25,m可取7个值,故在b转动一周的过程中,a、b、c共线14次,C错误,D正确。
15.如图所示,A是地球同步卫星,另一个卫星B的圆轨道位于赤道平面内,距离地面高度为h。已知地球半径为R,地球自转角速度为ω0,地球表面的重力加速度为g,O为地球中心。
(1)卫星B的运行周期是多少?
(2)如果卫星B的绕行方向与地球自转方向相同,某时刻A、B两卫星相距最近(O、B、A在同一直线上),求至少再经过多长时间,它们再一次相距最近?
答案 (1)2πR2g (2)-ω0
解析 (1)由万有引力定律和向心力公式得
G(R+h)2=mB(R+h), ①
GR2=mg, ②
联立①②解得 TB=2πR2g。 ③
(2)由题意得(ωB-ω0)t=2π ④
由③得 ωB=(R+h)3⑤
代入④得t=-ω0。
考点4 双星模型
1.双星模型
(1)模型构建
绕相同圆心转动的两个星体组成的系统,称之为双星系统,如图所示.
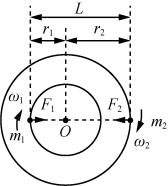
(2)特点
①各自所需的向心力由彼此间的万有引力提供,L2=m1ω1r1,L2=m2ω2r2.
②两颗星的周期及角速度都相同,T1= T2,ω1=ω2.
③两颗星的轨道半径与它们之间的距离关系为r1+r2=L.
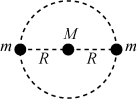
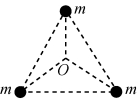
2.多星模型
(1)模型构建
所研究星体的万有引力的合力提供做圆周运动的向心力.除中央星体外,各星体的角速度或周期相同.
(2)三星模型
①三颗星体位于同一直线上.两颗质量相等的环绕星围绕中央星在同一半径为R的圆形轨道上运行,如图甲所示.
②三颗质量均为m的星体位于等边三角形的三个顶点上,如图乙所示.
甲
乙
丙
丁
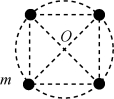
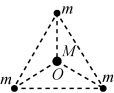
(3)四星模型
①其中一种是四颗质量相等的星体位于正方形的四个顶点上,沿着外接正方形的圆形轨道做匀速圆周运动,如图丙所示.
②另一种是三颗质量相等的星体始终位于等边三角形的三个顶点上,另一颗位于中心O,外围三颗星绕O做匀速圆周运动,如图丁所示.
16.(多选)天文学家通过观测两个黑洞并合的事件,间接验证了引力波的存在。该事件中甲、乙两个黑洞的质量分别为太阳质量的36倍和29倍,假设这两个黑洞绕它们连线上的某点做圆周运动,且两个黑洞的间距缓慢减小。若该双星系统在运动过程中,各自质量不变且不受其他星系的影响,则关于这两个黑洞的运动,下列说法正确的是( )
A.甲、乙两个黑洞运行的线速度大小之比为36∶29
B.甲、乙两个黑洞运行的角速度大小始终相等
C.随着甲、乙两个黑洞的间距缓慢减小,它们运行的周期也在减小
D.甲、乙两个黑洞做圆周运动的向心加速度大小始终相等
答案 BC
解析 由牛顿第三定律知,两个黑洞做圆周运动的向心力大小相等,它们的角速度ω相等,由Fn=mω2r可知,甲、乙两个黑洞做圆周运动的半径与质量成反比,由v=ωr知,线速度之比为29∶36,A错误,B正确;设甲、乙两个黑洞质量分别为m1和m2,轨道半径分别为r1和r2,有()r1+r22=m1T2r1,()r1+r22=m2T2r2,联立可得4π2=()()Gm1+m2,C正确;甲、乙两个黑洞做圆周运动的向心力大小相等,由牛顿第二定律a=m可知,甲、乙两个黑洞的向心加速度大小a1∶a2=29∶36,D错误。
17.(多选)根据科学家们的推测,双星的运动是产生引力波的来源之一。假设宇宙中有一由a、b两颗星组成的双星系统,这两颗星绕它们连线上的某一点在万有引力作用下做匀速圆周运动,测得a星的周期为T,a、b两星间的距离为l,轨道半径之差为Δr,已知a星的轨道半径大于b星的轨道半径,则( )
A.b星的周期为l+ΔrT
B.b星的线速度大小为()T
C.a、b两星的轨道半径之比为l-Δr
D.a、b两星的质量之比为l+Δr
答案 BD
解析 两颗星绕它们连线上的某一点在万有引力作用下做匀速圆周运动,所以两颗星的周期相等,则Tb=Ta=T,A错误。a、b两星间的距离为l,轨道半径之差为Δr,已知a星的轨道半径大于b星的轨道半径,则ra+rb=l、ra-rb=Δr,所以ra=2、rb=2。a、b两星的轨道半径之比rb=l-Δr,b星的线速度大小vb=T=()T,B正确,C错误。两颗星绕它们连线上的某一点在万有引力作用下做匀速圆周运动,则Gl2=maraT2=mbrbT2,所以a、b两星的质量之比mb=ra=l+Δr,D正确。
18.由于潮汐等因素影响,月球以每年约3~5cm 的速度远离地球.地球和月球可以看作双星系统,它们绕O点做匀速圆周运动.多年以后,地球( )
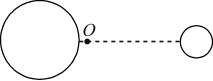
A.与月球之间的万有引力变大
B.绕O点做圆周运动的周期不变
C.绕O点做圆周运动的角速度变小
D.绕O点做圆周运动的轨道半径变小
答案 C
解析 多年以后,地球和月球间距离变大,两星的质量不变,由万有引力定律可知,地球与月球之间的万有引力变小,故A错误;地球和月球绕O点做匀速圆周运动的角速度大小ω相等,周期T相等,设地球与月球的质量分别为M1和M2,圆周运动的半径分别为r1和r2,地球和月球间距离为L,则有L=r1+r2,由万有引力提供向心力,得L2=M1Tr1=M1ω2r1,L2=M2T2r2=M2ω2r2,联立可得L2=T2=ω2L,r1=M1+M2,地球与月球的质量不变,地球和月球间距离增大,地球绕O点做圆周运动的周期T变大,地球绕O点做圆周运动的角速度变小,地球绕O点做圆周运动的轨道半径变大,故B、D错误,C正确.
19.太阳系以外存在着许多恒星与行星组成的双星系统,它们运行的原理可以理解为:质量为m0的恒星和质量为m的行星(m0>m),在它们之间的万有引力作用下有规律地运动着。如图所示,我们可认为行星在以某一定点C为中心、半径为a的圆周上做匀速圆周运动(图中没有表示出恒星)。设引力常量为G,恒星和行星的大小可忽略不计。
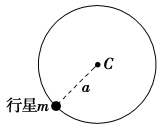
(1)试在图中粗略画出恒星运动的轨道和位置。
(2)试计算恒星与点C间的距离和恒星的运行速率v。
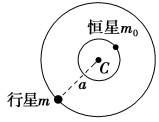
答案 (1)见解析图 (2)m0a m0+ma
解析 (1)恒星运动的轨道和位置大致如图。
(2)对行星m有
F=mω2Rm, ①
对恒星m0有
F′=m0ω2Rm0, ②
根据牛顿第三定律,F与F′大小相等
由①②得Rm0=m0a,
对恒星m0有Rm0=G(Rm+Rm0)2,
代入数据得v=m0+ma。
20.如图所示,质量分别为m和M的两个星球A和B在引力作用下都绕O点做匀速圆周运动,星球A和B两者中心之间的距离为L。已知A、B的中心和O点始终共线,A和B分别在O点的两侧。引力常量为G。
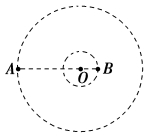
(1)求两星球做圆周运动的周期T。
(2)在地月系统中,若忽略其他星球的影响,可以将月球和地球看成上述星球A和B,月球绕其轨道中心运行的周期记为T1。但在近似处理问题时,常常认为月球是绕地心做圆周运动的,这样算得的运行周期为T2。已知地球和月球的质量分别为5.98×1024 kg和7.35×1022 kg。求T2与T1的二次方的比值。(结果保留三位小数)
答案 (1)2πG(M+m) (2)1.012
解析 (1)由题意可知,星球A和B为双星模型,A和B有相同的角速度和周期。
设A、B做圆周运动的半径分别为r、R,则有mω2r=Mω2R,r+R=L,
联立解得R=M+mL,r=M+mL。
对A,根据向心力公式和万有引力定律得
L2=mTM+mL,
解得T=2πG(M+m)。
(2)设地球质量为M,月球质量为m,地球、月球中心之间的距离为L′,由题意知,可以将地月系统看成双星系统,
由(1)得T1=2πG(M+m)。
若认为月球绕地心做圆周运动,则根据向心力公式和万有引力定律得L′2=mT2L′,解得T2=2πGM。
所以T2与T1的二次方的比值为T1=M=5.98×1024≈1.012。
附件 (1个)
1、本网站所提供的信息,只供教育教学参考之用。
2、本网站及其会员一概毋须以任何方式就任何信息传递或传送的失误、不准确或错误对用户或任何其他人士负任何直接或间接的责任。
3、在法律允许的范围内,本网站在此声明,不承担用户或任何人士就使用或未能使用本网站所提供的信息或任何链接或项目所引致的任何直接、间接、附带、从属、特殊、惩罚性或惩戒性的损害赔偿。
4、访问者在从事与本网站相关的所有行为(包括但不限于访问浏览、利用、转载、宣传介绍)时,必须以善意且谨慎的态度行事;访问者不得故意或者过失的损害本网站的各类合法权益,不得利用本网站以任何方式直接或者间接的从事违反中华人民共和国法律、国际公约以及社会公德的行为。对于访问者利用本网站提供的信息而作出的任何决策、决定以及其后果,本网站不承担任何责任
5、本网站图片,文字之类版权,本网站无法鉴别所上传图片或文字的知识版权,如果侵犯,请及时通知我们,本网站将在第一时间及时删除。
6、凡以任何方式登录本网站或直接、间接使用本网站资料者,视为自愿接受本网站声明的约束。
GYEDU
